Minimo Comun Multiplo Y Maximo Comun Divisor Para Niños – El Mínimo Común Múltiplo (MCM) y el Máximo Común Divisor (MCD) son conceptos fundamentales en matemáticas que ayudan a los niños a resolver problemas y comprender las relaciones entre los números. En este artículo, exploraremos estos conceptos, sus métodos de cálculo y sus aplicaciones prácticas.
El MCM es el número más pequeño que es múltiplo de dos o más números dados, mientras que el MCD es el número más grande que divide a dos o más números sin dejar resto.
Definición de Mínimo Común Múltiplo (MCM) y Máximo Común Divisor (MCD)

El Mínimo Común Múltiplo (MCM) de dos o más números es el número positivo más pequeño que es múltiplo de todos los números dados. El Máximo Común Divisor (MCD) de dos o más números es el número positivo más grande que divide a todos los números dados sin dejar resto.
Cómo encontrar el MCM
Para encontrar el MCM de dos o más números, podemos seguir estos pasos:
- Encontrar los factores primos de cada número.
- Identificar los factores primos comunes y no comunes.
- Multiplicar los factores primos comunes y no comunes para obtener el MCM.
Por ejemplo, para encontrar el MCM de 12 y 18, encontramos sus factores primos:
- = 2 x 2 x 3
- = 2 x 3 x 3
Los factores primos comunes son 2 y
- Los factores primos no comunes son 2 y
- Por lo tanto, el MCM de 12 y 18 es:
MCM = 2 x 2 x 3 x 3 = 36
Cómo encontrar el MCD
Para encontrar el MCD de dos o más números, podemos seguir estos pasos:
- Encontrar los factores primos de cada número.
- Identificar los factores primos comunes.
- Multiplicar los factores primos comunes para obtener el MCD.
Por ejemplo, para encontrar el MCD de 12 y 18, encontramos sus factores primos:
- = 2 x 2 x 3
- = 2 x 3 x 3
Los factores primos comunes son 2 y
Por lo tanto, el MCD de 12 y 18 es:
MCD = 2 x 3 = 6
Métodos para encontrar el MCM y el MCD

Existen varios métodos para encontrar el Mínimo Común Múltiplo (MCM) y el Máximo Común Divisor (MCD) de dos o más números. Los métodos más comunes son la factorización prima y la división larga.
Método de la factorización prima
Este método implica factorizar cada número en sus factores primos y luego identificar los factores primos comunes. El MCM es el producto de todos los factores primos comunes y no comunes, mientras que el MCD es el producto de los factores primos comunes.
Por ejemplo, para encontrar el MCM y el MCD de 12 y 18, factorizamos cada número:
“`
- = 2 x 2 x 3
- = 2 x 3 x 3
“`
Los factores primos comunes son 2 y 3. Por lo tanto, el MCM es 2 x 2 x 3 x 3 = 36 y el MCD es 2 x 3 = 6.
Método de la división larga
Este método implica dividir el número más grande entre el más pequeño y continuar dividiendo el divisor anterior entre el resto hasta que el resto sea 0. El último divisor es el MCD.
Para encontrar el MCM, multiplicamos el MCD por el cociente de la división.
Por ejemplo, para encontrar el MCM y el MCD de 24 y 36, dividimos 36 entre 24:
“` 36 ÷ 24 = 1 resto 12 24 ÷ 12 = 2 resto 0“`
Por lo tanto, el MCD es 12. Para encontrar el MCM, multiplicamos el MCD por el cociente 1: 12 x 1 = 12. Por lo tanto, el MCM es 12.
Aplicaciones del MCM y el MCD
El Mínimo Común Múltiplo (MCM) y el Máximo Común Divisor (MCD) son conceptos matemáticos que tienen numerosas aplicaciones en la resolución de problemas. Aquí exploraremos cómo se utilizan en fracciones y expresiones algebraicas, junto con ejemplos prácticos de su uso.
Uso en fracciones
El MCM es útil para sumar y restar fracciones con diferentes denominadores. Al encontrar el MCM, podemos crear un denominador común para las fracciones, lo que permite combinarlas y simplificar la operación. Por ejemplo, para sumar 1/2 y 1/4, primero encontramos el MCM de 2 y 4, que es 4. Luego convertimos las fracciones a 2/4 y 1/4, y las sumamos como 3/4.El
MCD, por otro lado, se utiliza para simplificar fracciones. Al encontrar el MCD del numerador y el denominador, podemos dividir ambos por ese valor para obtener una fracción equivalente en su forma más simple. Por ejemplo, para simplificar 12/18, encontramos el MCD de 12 y 18, que es 6. Dividiendo ambos por 6, obtenemos la fracción simplificada 2/3.
Uso en expresiones algebraicas, Minimo Comun Multiplo Y Maximo Comun Divisor Para Niños
El MCM y el MCD también se utilizan en la simplificación de expresiones algebraicas. El MCM se utiliza para factorizar expresiones con términos comunes. Por ejemplo, para factorizar 12x + 18y, encontramos el MCM de 12 y 18, que es 36. Luego factorizamos ambos términos por 3, obteniendo 6(2x + 3y).El
MCD se utiliza para cancelar factores comunes en expresiones fraccionarias. Por ejemplo, para simplificar (x^2
- 1) / (x + 1), encontramos el MCD de x^2
- 1 y x + 1, que es x
- 1. Dividiendo ambos términos por x
- 1, obtenemos la expresión simplificada x + 1.
Aplicaciones prácticas
Además de su uso en matemáticas, el MCM y el MCD tienen aplicaciones prácticas en varios campos. Por ejemplo, en ingeniería, se utilizan para calcular el período más corto en el que dos engranajes encajarán perfectamente. En música, se utilizan para determinar el ritmo común entre dos melodías.
En cocina, se utilizan para escalar recetas para diferentes cantidades de porciones.
Ejemplos y ejercicios
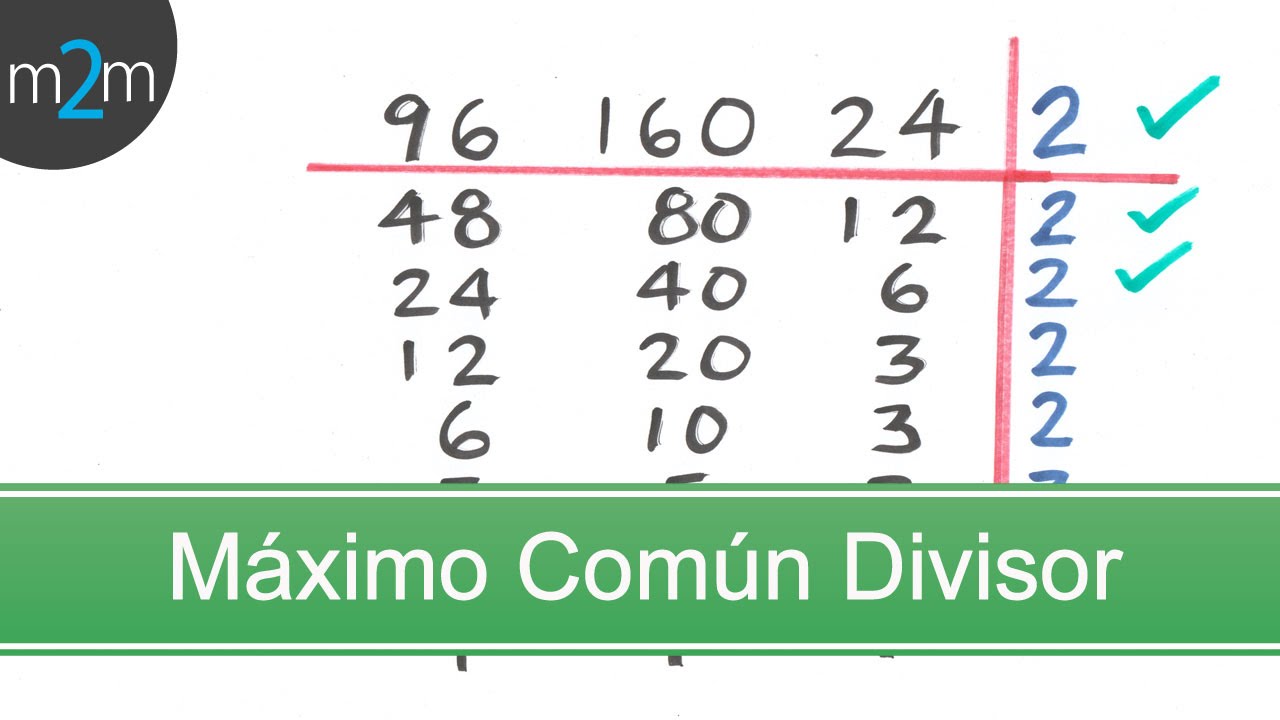
Los siguientes ejemplos y ejercicios ayudarán a los niños a comprender y practicar los conceptos de Mínimo Común Múltiplo (MCM) y Máximo Común Divisor (MCD).
Ejemplos
Tabla de ejemplos de MCM y MCD:
| Números | MCM | MCD |
|---|---|---|
| 6, 9 | 18 | 3 |
| 12, 15 | 60 | 3 |
| 10, 20 | 20 | 10 |
| 16, 24 | 48 | 8 |
| 21, 28 | 84 | 7 |
Ejercicios
Lista de ejercicios para encontrar el MCM y el MCD:
- Encuentra el MCM y el MCD de 12 y 18.
- Calcula el MCM y el MCD de 20 y 30.
- Determina el MCM y el MCD de 15 y 25.
- Halla el MCM y el MCD de 16 y 24.
- Encuentra el MCM y el MCD de 21 y 28.
Trucos y atajos: Minimo Comun Multiplo Y Maximo Comun Divisor Para Niños

Existen algunos trucos y atajos que pueden ayudar a encontrar el MCM y el MCD de manera rápida y eficiente.
Uno de los atajos más útiles es el algoritmo de Euclides, que se utiliza para encontrar el MCD de dos números. El algoritmo funciona mediante la repetición de la siguiente operación:
- Dividir el número mayor por el número menor.
- Tomar el resto de la división y dividir el número menor por el resto.
- Repetir los pasos 1 y 2 hasta que el resto sea 0.
- El último divisor no nulo es el MCD de los dos números.
Por ejemplo, para encontrar el MCD de 12 y 18, seguiríamos estos pasos:
- 18 ÷ 12 = 1, resto 6
- 12 ÷ 6 = 2, resto 0
Por lo tanto, el MCD de 12 y 18 es 6.
Tabla de trucos y atajos
| Truco/Atajo | Descripción |
|---|---|
| Factorización prima | Factorizar ambos números en sus factores primos y luego multiplicar los factores comunes. |
| Algoritmo de Euclides | Un algoritmo paso a paso para encontrar el MCD de dos números. |
| MCD de números consecutivos | El MCD de dos números consecutivos siempre es 1. |
| MCD de un número y cero | El MCD de un número y cero es el propio número. |
El MCM y el MCD son herramientas esenciales para resolver problemas matemáticos, desde simplificar fracciones hasta resolver ecuaciones algebraicas. Comprender estos conceptos ayuda a los niños a desarrollar habilidades de pensamiento crítico y a apreciar la belleza de la aritmética.
